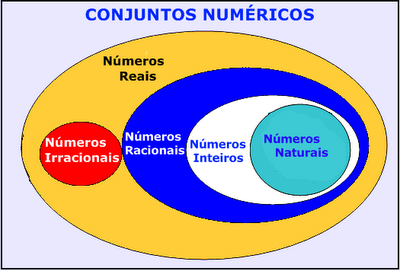
Conjutos Numéricos

É preciso saber onde cada número está localizado. São eles:

Conjuntos dos Números Naturais:

N= {0,1,2,3,4,5,6,7,8,9,10,...}

Conjuntos dos Números Inteiros:

Z={...,-5,-4-3,-2,-1,0,1,2,3,4,5,...}

Conjuntos dos Números Racionais:

Q={ a/b | "a" pertence aos números inteiros; "b" pertence aos números inteiros e diferente de zero}  » As dízimas periódicas fazem parte desse conjunto.   Ex.: 3,444... ; 2,3535...

Conjuntos dos Números Irracionais:

Olhe esse número: 4,47213595...

Esse número é uma seqüência decimal ilimitada e não-periódica. Então é chamado de número irracional. Representamos o conjunto dos números irracionais por “I”.

 Raiz quadrada de 2 =1,414213562...

Raiz quadrada de 5 =2,236067978...

Pi =3,141592654...

Conjuntos dos Números Reais:

É formado por todos os conjuntos vistos anteriormente. O conjunto dos números reais é representado por ”R”

Fração Geratriz da Dízima Periódica:

A fração geratriz periódica simples é formada por uma fração que terá como numerador os algarismos que formam o período e como denominador um número formado por tantos noves forem os algarismos do período.

Obs.: o número inteiro soma-se com a fração.

Ex.: 0,222...= 2/9                                                 2,555...=2+5/9 =23/9

       0,121212...=12/99=4/33                               5,232323...=5+23/99 = 518/99                             

       0,123123123...=123/999=41/333                 3,444...=3+4/9

A fração geratriz periódica composta é formada por uma fração que terá como numerador o número formado pela não-periódica e pela parte periódica, subtraído pela parte não-periódica e o denominador será um número formado de tantos noves quantos forem os algarismos da parte periódica, seguidos de tantos zeros quantos forem os algarismos da parte não-periódica.

Obs.: o número inteiro soma-se com a fração.

Ex.:    0,1444... = 14/90 - 1/90 =  13/90

          2,35717171... = 23571/9900 - 235/9900 = 5834/2475

          0,23555... = 235/900 - 23/900 = 53/225                                                                   

Outra maneira de resolução das geratrizes composta:

Ex.: 0,1444....

1° passo: chamamos de x.

X=0.1444...

2° passo: observar quantidade de algarismos não-periódicos e multiplicar os dois membros por 1 acrescentado por zeros, dependendo da quantidade de algarismos.

10x=1,444...

3° passo: observar a quantidade de algarismos periódicos e multiplicar os dois membros por 1 acrescentado por zeros, dependendo da quantidade de algarismos.

100x=14,444...

4° passo: subtrair o 3° passo  pelo 2° passo e resolver a equação restante.

100x=14,444...

 10x=  1,444...

90x=13

    x=13/90

Obs.: para resolver as geratrizes simples, pula o 2°passo.

Ex.: 0,222...

     x=0,222...

 10x=2,222...

   9x=2

     x=2/9